欧拉公式_欧拉公式的证明

欧拉公式_欧拉公式的证明

       欧拉公式是一个非常重要的话题，可以从不同的角度进行思考和讨论。我愿意与您分享我的见解和经验。

1.什么是欧拉公式

2.欧拉公式的三种形式

什么是欧拉公式

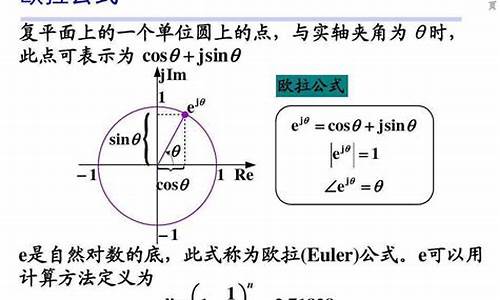
       欧拉公式是欧哈德·欧拉在十八世纪创造的，是数学界最着名、最美丽的公式之一。之所以如此，是因为它涉及到各种显然非常不同的元素，比如无理数e、虚数和三角函数。复变函数中，e^(ix)=(cos x+isin x)称为欧拉公式，e是自然对数的底，i是虚数单位。

欧拉公式有4条，分别是：

1、分式

       a＾r/（a-b）（a-c）+b＾r/（b-c）（b-a）+c＾r/（c-a）（c-b）

       当r=0，1时式子的值为0；当r=2时值为1；当r=3时值为a+b+c。

2、复数

       由e＾iθ=cosθ+isinθ，得到：sinθ=（e＾iθ-e＾-iθ）/2i；cosθ=（e＾iθ+e＾-iθ）/2此函数将两种截然不同的函数---指数函数与三角函数联系起来，被誉为数学中的“天桥”。

       当θ=π时，成为e＾iπ+1=0 它把数学中最重要的e、i、π、1、0联系起来了。

3、三角形

       设R为三角形外接圆半径，r为内切圆半径，d为外心到内心的距离，则：d＾2=R＾2-2Rr。

4、多面体

       设v为顶点数，e为棱数，f是面数，则v-e+f=2-2p。

       p为亏格，2-2p为欧拉示性数，例如p=0 的多面体叫第零类多面体； p=1 的多面体叫第一类多面体。

欧拉公式的三种形式

       欧拉公式推导如下：

        1. 欧拉公式是e^ix=cosx+isinx, e是自然对数的底，I是虚数单位。将三角函数的定义域扩展到复数，建立了三角函数与指数函数的关系。它在复变函数理论中起着非常重要的作用。

        2. e^ix=cosx+isinx的证明:因为e^x=1+x/1+ x^2/2!+ x ^ 3/3 !+ x ^ 4/4 !+?因为x = 1 - x ^ 2/2 !+ x ^ 4/4 !- x ^ 6/6 !?sin (x) = x ^ 3/3 !+ x ^ 5/5 !- x ^ 7/7 !......在e^x的展开中，用?IX代替x。(?i)?=-1，(?i)?=?I，(?I)^4=1 ...... e^?ix=1?ix/1!- x ^ 2/2 ! x ^ 3/3 !+ x ^ 4/4 !...... = ( 1 - x ^ 2/2 !+?)?I (X -x^3/3!?)所以e^ix =cosx?isinx将公式中的X替换为-x得到:e^-ix=cosx isinx，然后将两个公式加减得到:sinx= (e^ix-e^-ix) / (2I)， cosx= (e^ix+e^-ix) /2这两个公式也称为欧拉公式。取e^ix中的X =cosx+isinx = ?，得到e^i ? +1=0。

       欧拉公式的三种形式如下：R+V-E=2，在任何一个规则球面地图上，用R记区域个数，V记顶点个数，E记边界个数，则R+V-E=2，这就是欧拉定理，它于1640年由Descartes首先给出证明，后来Euler于1752年又独立地给出证明，我们称其为欧拉定理，在国外也有人称其为Descartes定理。

       欧拉公式又称为欧拉定理，也称为尤拉公式，是用在复分析领域的公式，欧拉公式将三角函数与复数指数函数相关联，之所以叫作欧拉公式，那是因为欧拉公式是由莱昂哈德·欧拉提出来的，所以用他的名字进行了命名。?

       尤拉公式提出，对任意实数?x，都存在其中?e是自然对数的底数，?i是虚数单位，而?\cos和?\sin则是余弦、正弦对应的三角函数，参数?x则以弧度为单位。这一复数指数函数有时还写作?{cis}(x)。由于该公式在?x为复数时仍然成立，所以也有人将这一更通用的版本称为尤拉公式。

       为什么欧拉公式被称为世界上最完美的公式了？

       欧拉公式的巧妙之处在于，它没有任何多余的内容，将数学中最基本的e、i、π放在了同一个式子中，同时加入了数学也是哲学中最重要的0和1，再以简单的加号相连。高斯曾经说：“一个人第一次看到这个公式而不感到它的魅力，他不可能成为数学家。”?虽然不敢肯定她是世界上“最伟大公式"，但是可以肯定它是最完美的数学公式之一。

       好了，今天关于“欧拉公式”的话题就讲到这里了。希望大家能够对“欧拉公式”有更深入的认识，并从我的回答中得到一些启示。如果您有任何问题或需要进一步的信息，请随时告诉我。